Generalizing from Data

Fernando Rios-Avila

Levy Economics Institute

August 23, 2024

Generalization

• Sometimes we analyze a dataset with the goal of learning about patterns in that dataset alone.
  • In such cases there is no need to generalize our findings to other datasets.
  • Example: We search for a good deal among offers of hotels, all we care about are the observations in our dataset.
• Often we analyze a dataset in order to learn about patterns that may be true in other situations.
  • We are interested in finding the relationship between our dataset and the situation we care about.
  • Example: Will the treatment we are studying work in other settings?

Generalization: Inference and External Validity

Generalization

• Goal: Generalize the results from a single dataset to other situations.

• The act of generalization is called inference: we infer something from our data about a more general sitatuation.

  • For this we want to test hypothesis based on our estimates (evidence)

• Two Things to consider

  1. Statistical inference: the process of using data (in hand) to infer the properties of a population. Identify general pattern.
  2. External validity: the extent to which our data represents the general pattern we care about in other settings.

Statistical inference

• There are several statistical methods to make inference.
• The general pattern (A model) is an abstract thing that may or may not exist.
• If we can assume that the general pattern exists, the tools of statistical inference can be very helpful.
  • If we find a positive relationship between two variables in our data, we can use statistical inference to say if the same relationship is likely in the population.

General patterns 1: Population and representative sample

• The cleanest example of representative data is a representative sample of a well-defined population.

• A sample is representative of a population if the distribution of all variables is very similar in the sample and the population. \[f(y,x,z,...)_{sample} \approx f(y,x,z,...)_{population}\]

• Random sampling is the best way to achieve a representative sample.

General patterns 2: No population but general pattern

• “Representation” is less straightforward in other setups.
• There isn’t a “population” from which a random sample was drawn on purpose.
  • Using the past to uncover a pattern of the future. (Time series)
  • Use analogy to generalize patterns on Products A into Products B. (requires external Validity)
• Instead, we should think of our data as one that represents a general pattern (a model).
  • \(X\beta\) exists, and each year is a random realization.
  • \(X\beta\) exists, and each product is a random version.
• You can think of a “general pattern” as the “true” model dictating the data.

External validity

• How likely is that what we learn is relevant other situations we care about?

• Are our findings unique to our data? or can they happen “out there”?

  • With external validity, our data can tell what to expect.
  • No external validity: whatever we learn from our data, may turn out to be not relevant at all.

• This has been a problem with RCTs in economics: the results are not always generalizable to other settings.

The process of inference

The process of inference:

1. Consider a statistic we may care about, such as the mean.
2. Compute its estimated value from a dataset.
3. Infer the value in the population, that our data represents.

It is good practice to divide the inference problem into two:

1. Use statistical inference to learn about the population the data represents.
2. Assess external validity: Assess how the data in hand represents the population we care about.

Stock market returns: Inference

• Task: Assess the likelihood of experiencing a loss of 5% on an investment portfolio from one day to the next
• Data: day-to-day returns on the S&P 500, from 25 August 2006 to 26 August 2016: 2,519 days.
• Finding: 0.5% of the days in the dataset have a loss of 5% or more.
• Inference problem:
  • How can we generalize this finding? What can we infer from this 0.5% chance for the next calendar year?

Repeated samples

Repeated samples

• Normally, There is one sample. But, theoretical framework assumes you could obtain many (repeated) samples. (Frequentist approach)
• The goal of statistical inference is learning the value of a statistic in the population represented by our data.
  • But, each repeated samples, would give a different value of the statistic.
• Because of the different values, the statistic obtained with repeated samples will have a distribution
  • This is the sampling distribution.
• The standard deviation of the sampling distribution is what is called the standard error of the statistic (typical error across random samples).

Repeated samples properties

The sampling distribution has three important properties:

1. Unbiasedness: The average of the values in repeated samples is equal to its true value (=the value in the entire population / general pattern).
2. Asymptotic normality: The sampling distribution is approximately normal. With large sample size, it is very very close.
3. Root-n convergence: The standard error (the standard deviation of the sampling distribution) is smaller the larger the samples, with a proportionality factor of the square root of the sample size.

Repeated samples

• Easier concept:
  • When data is sample from a well-defined population - many other samples could have turned out instead of what we have.
  • Example: Mexican firms - random sample - population of firms.
• Harder concept:
  • Some times there is no clear definition of population. (but there is a model).
  • Data of returns on an investment portfolio is as a particular realization of the history of returns that could have turned out differently.
    • Multiverse: many possible histories of returns, we see only one.

Case study

Stock market returns: A simulation

• We can not rerun history many many times…
• So we will run a Simulation exercise - to better understand how repeated samples work.
• Suppose the 11-year dataset is the population - the fraction of days with 5%+ losses is 0.5% in the entire 11 years’ data. That’s the true value.
• We assume we have only 500 days of daily returns in our dataset.
• Task: estimate the true value of the fraction in the 11-year period from the data we have using a simulation exercise.

Stock market returns: A simulation

use data_slides/sp500.dta, clear
gen return = (value - value[_n-1])/value[_n-1]
gen lost5 = return < -0.05
set seed 1

** Simulation
gen mn_lost5=.
forvalues i = 1/1000 {
    preserve
      qui:sample 500, count
      sum lost5 , meanonly
    restore
    qui:replace mn_lost5 = r(mean) in `i'
}

Stock market returns: A simulation

(start=0, width=.002)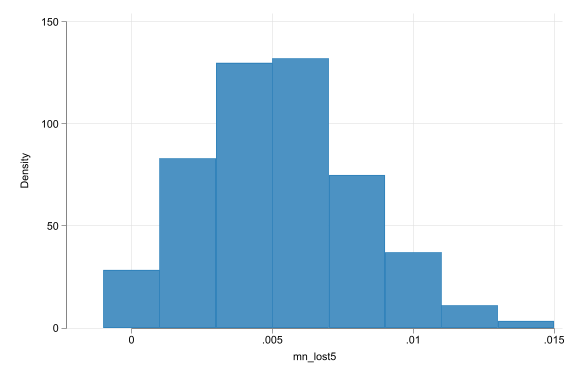

Measuring uncertainty

How bad is the error in our estimate?

The standard error and the confidence interval

• Confidence interval (CI) is a measure of statistical inference that allows some margin of error.
• The CI defines a range where we can expect the true value in the population, with a probability.
• Probability tells how likely it is that the true value is in that range, if we were to draw many repeated samples.

If E(X) and SE(X) are known

• If we know the true value of a statistic and its standard error, then we can calculate the CI.
  • The CI is centered around the true value of the statistic.
  • This CI is the range of values that we can expect the sample statistic to fall in, with a certain probability.
  • for example, 95% CI: the sample statistic will fall within the CI in 95% of the repeated samples.
  • But in 5% of the cases, the sample statistic will fall outside the CI.

If E(X) and SE(X) are not known

• When we say “95% CI”, we mean that if we were to draw many repeated samples, the true value would fall within the CI in 95% of the cases.
• However, it also means that in 5% of the cases, the true value would fall outside the CI.
  • This means, some times (5% of the cases) we will be wrong.

Confidence interval

• CI is almost always symmetric around the estimated value of the statistic in our dataset. (if we assume normality of the sampling distribution)

• How to calculate the CI?

  • Get estimated value.
  • Define probability, confidence level (Say 95%).
  • Calculate CI with the use of SE. \[95\% CI= \hat\mu \pm 1.96SE\]

• Under Normality, 90% CI is the ±1.645SE interval, the 99 % CI is the ±2.576SE.

• But we commonly use the rule of 2: ±2SE.

Calculating the standard error

• Estimating the sample mean \(\bar{x}\) is easy. But how do we estimate the standard error?
  • In reality, we don’t get to observe the sampling distribution. Instead, we observe a single dataset.
  • That dataset is one of many potential samples that could have been drawn from the population.
• Good news: We can get a very good idea of how the sampling distribution would look like - good estimate of the standard error - even from a single sample.
• Getting SE – Option 1: Use a formula. \(\leftarrow\) Theoretical approach.
• Getting SE – Option 2: Simulate \(\leftarrow\), The bootstrap method.

Calculating the standard error

Consider the statistic of the sample mean.

• Assume the values of \(x\) are independent across observations in the dataset.
• \(\bar{x}\) is the estimate of the true mean value of \(x\) in the population.
• Assume sampling distribution is approximately normal, with the true value as its mean.

The standard error formula for the estimated \(\bar{x}\) is \[SE (\bar{x}) = \frac{1}{\sqrt{n}} Std[x]\]

where \(Std[x]\) is the standard deviation of the variable \(x\) in the data and \(n\) is the number of observations in the data.

The standard error formula

• The standard error is larger…
  • the larger the standard deviation of the variable.
  • the smaller the sample
• The larger the standard error, the wider the confidence interval, and the less precise the estimate (wider CI).

External validity

External validity

• In statistical inference the CI represents the uncertainty about the true value of the statistic in the population that our data represents.
• But What is the population, we care about? How close is our data to this?
• External validity: Can we generalize the pattern we found in our data to other situations?
• High external validity: if our data is close to the population.
• External validity is as important as statistical inference, but it is not a statistical question.

External validity

• The three most important challenges to external validity are:
  • Time: we have data on the past, but we care about the future.
  • Space: our data is on one country, but interested how a pattern would hold elsewhere in the world.
  • Sub-groups: our data is on 25-30 year old people. Would a pattern hold on younger / older people?

External validity: Portafolio Example

• Daily 5%+ loss probability with a 95% CI [0.2, 0.8] in our sample. This captures uncertainty.
• External Validity: Would this data be representative of the events of one year in the future?
  • Probably not, because the future is uncertain.
  • Our data: 2006-2016 dataset includes the financial crisis and great recession of 2008-2009. uncertain if the future will have similar events.
• Hence, the real CI is likely to be substantially wider.

External validity: Managers Example

• Manager and firm size evidence in Mexico.
• How to think about external validity?
  • Would the same patterns hold in other countries? Develped countries? Emerging markets?
  • Would the same patterns hold in other sectors? Other industries?
• Only Mexico? only firms of a certain size?

The bootstrap

The bootstrap

• Bootstrap is a method to create synthetic samples that are similar but different.
• An method that is very useful in general.
  • The method you use, when you don’t know…
• It is essential for many advanced statistics applications such as machine learning.
• The bootstrap is a method to estimate uncertainty in a statistic, that uses the data itself.

to lift oneself by one’s bootstraps

The bootstrap

• The bootstrap method takes the original dataset and draws many repeated samples (with replacement) of the size of that dataset.

• Say you have a dataset of 10 observations, named 1, 2, 3, …, 10.

  • Bootstrap sample 1: 2, 5, 5, 7, 8, 9, 9, 9, 10, 10.
  • Bootstrap sample 2: 1, 1, 2, 3, 4, 5, 6, 7, 8 , 9.
  • And so on, repeated many times.

• Each new sample is called a bootstrap sample.

The bootstrap

• a Bsample is (almost) always the same size as the original dataset.
• Some Data is repeated, some is left out.
• Typically, we require between 500-10,000 bootstrap samples. (Stata’s default is 50)
• Computationally intensive, but feasible

The bootstrap method: How does it work?

• For each BSample, you estimate the statistic of interest. (e.g. mean)
• The distribution of the statistic across these repeated bootstrap samples is a good approximation to the sampling distribution.
• In this case, the bootstrap Standard Error is the standard deviation of the statistic across the bootstrap samples.
• Also, the 95% CI is the 2.5th and 97.5th percentiles of the distribution of the statistic across the bootstrap samples. Or you can use the estimated SE.

Stock market returns: The Bootstrap standard error

Stata Corner

Bootstraping in Stata can be easy. Most commands have a built-in bootstrap option. Otherwise, we can program it!

display "Bootstrap"
bootstrap mean=r(mean), nowarn reps(1000) seed(1) dots(100): sum lost5, meanonly
est sto m1
display "Formula"
mean lost5
est sto m2

Stock market returns: The Bootstrap standard error

Stata Corner

			Mean
Formula	0.0052	[0.0023,0.0080]
Bootstrap			0.0052	[0.0024,0.0080]
N	2519		2519

Generalization - Summary

• Generalization is a key task - finding beyond the actual dataset.
• This process is made up of discussing statistical inference and external validity.
• Statistical inference generalizes from our dataset to the population using a variety of statistical tools.
• External validity is the concept of discussing beyond the population for a general pattern we care about; an important but typically somewhat speculative process.

Break

Hypothesis Testing

Motivation

• The internet allowed the emergence of specialized online retailers while brick-and-mortar shops also sell goods on the main street. How to measure price inflation in the age of these options?
• To help answer this, we can collect and compare online and offline prices of the same products and test if they are the same.

Hypothesis Testing

The truth is out there, but its unknowable.

The logic of hypothesis testing

• A hypothesis is a statement about the population parameter, of which we are not sure if true or not.
• Hypothesis testing = analyze our data to make a decision on the hypothesis
• Reject the hypothesis if there is enough evidence against it.
• Don’t reject it if there isn’t enough evidence against it.
  • But NEVER accept it as true.
• Important asymmetry here: rejecting a hypothesis is a more conclusive decision than not rejecting it.

Inference

• Testing a hypothesis: making inference with a focus on a specific statement.
  • Hypothesis: It is cheaper to buy online than offline.
• Can answer questions about the population represented by our data.
• But, It is an inference: have to assess external validity.

The setup

• Define the the statistic we want to test, \(s\) (e.g. mean).
• We are interested in the true value of \(s\), \(s_{true}\).
  • This implies the true value in the population.
• The value of the statistic in our data is its estimated value, denoted by a hat on top \(\hat{s}\).

Hypothesis testing: H0 vs HA

• Need to formally state the question as two competing hypotheses of which only one can be true:
  • a null hypothesis \(H_0\) and an alternative hypothesis \(H_a\).
• They are formulated in terms of the unknown true value of the statistic. (we now the sample value)
• Together they cover all possibilities.

\(H_0\): Online and offline prices are the same. \(H_a\): Online and offline prices are different.

The Null is protected

Innocent (H0) until proven guilty (Ha)

• Testing a hypothesis \(H_0\)= see if there is enough evidence in our data to reject the null.

• The null is protected: We start assuming the Null is true

  • If we have strong evidence against it, we reject it
  • If not, we don’t reject it.

Types of testing: \(H_0\) vs \(H_a\)

• There are two types of Hypothesis:
  • Two-sided alternative: We are interested if the true value of the statistic is different from the hypothesized value.

\[H_0: \theta = 42 \ \ vs \ \ H_A: \theta \neq 42\]

• One-sided alternative: We are interested if the true value of the statistic is greater or smaller than the hypothesized value. \[H_0: \theta \leq 42 \ \ vs \ \ H_A: \theta > 42\]

The logic of hypothesis testing

• \(H_A\) is (often) what I want to prove
• \(H_0\) is what I wanna reject so that we can prove \(H_A\)
• \(H_0\) is not rejected
  • not enough evidence or
  • true (ie \(H_A\) is false)
• I can never say \(H_0\) is true.

Case Study - online vs offline prices

• Question: Do the online and offline prices of the same products differ?
• This data includes 10 to 50 products in each retail store included in the survey (the largest retailers in the U.S. that sell their products both online and offline).
• The products were selected by the data collectors in offline stores, and they were matched to the same products the same stores sold online.
• The statistic of interest is the difference in average prices.

• Each product \(i\) has an off-line and on-line price.

• The statistic with \(n\) observations (products) in the data, is: \[s = \bar{p}_\text{diff} = \frac{1}{n} \sum_{i=1}^n (p_{i,\text{online}} - p_{i,\text{offline}})\]

• The average of the price differences is equal to the difference of the average prices \[\frac{1}{n} \sum_{i=1}^n (p_{i,\text{online}} - p_{i,\text{offline}}) = \frac{1}{n} \sum_{i=1}^n p_{i,\text{online}} - \frac{1}{n} \sum_{i=1}^n p_{i,\text{offline}}\]

Descriptive statistics of the difference:

• The mean difference is USD -0.05: online prices are, on average, 5 cents lower in this dataset.
• Spread around this average: Std: USD 10
• Extreme values matter: Range: -380 — USD +415.
• Of the 6439 products, 64% have the same online and offline price, for 87%, the difference within ±1 dollars.

Case Study - External validity:

• The products in the data may not represent all products sold at these stores.
  • Bias? Were the products selected randomly?
• Strictly: The findings refer to products sond online-offline by large retail stores. And those selected by the people collecing the data.
• More broadly: price differences among all products in the U.S. sold both online and offline by the same retailers.
  • May not be representative of smaller retailers

Testing

Good old t-test

T-test

• The t-test is the testing procedure based on the t-statistic
• We compare the estimated value of the statistic \(\hat{s}\) to zero. (\(H_0\))
• Evidence to reject the null is based on difference between \(\hat{s}\) and zero.
  • Reject the null if difference large (its un unlikely to be zero).
  • Not reject the null if the difference is small ( not enough evidence against it).

T-test

• The test statistic is a statistic that measures the (standardized) distance of the estimated value from what the true value would be if \(H_0\) was true.
• Uses estimated value of \(s\) (\(\hat{s}\)) and the standard error of estimate (SE (\(\hat{s}\))).
• Consider \(H_0: s_\text{true} = 0, H_A: s_\text{true} \neq 0\). The t-statistic for this hypotheses is: \[t = \frac{\hat{s}}{\text{SE}(\hat{s})}\]

T-test

When \(\hat{s}\) is the average of a variable \(x\), the t-statistic is simply \[t = \frac{\bar{x}}{\text{SE}(\bar{x})}\]

When \(\hat{s}\) is the average of a variable \(x\) minus a number, the t-statistic is \[t = \frac{\bar{x} - \text{number}}{\text{SE}(\bar{x})}\]

When \(\hat{s}\) is the difference between two averages, say, \(\bar{x}_A\) and \(\bar{x}_B\), the t-statistic is \[t = \frac{\bar{x}_A - \bar{x}_B}{\text{SE}(\bar{x}_A - \bar{x}_B)}\]

T-test

• While we can use SE to calculate the t-statistic, SE may be more difficult to calculate in some situations.

  • Different samples, different SE, etc

• Some times you may want to use Bootstrap to calculate SE.

• Stata Corner: ttest command in Stata calculates the t-statistic for a difference in means.

Generalization

Making a decision

• Once you obtain your t-statistic (or other relevant statistic), you need to make a decision regarding the null hypothesis.
• In hypothesis testing the decision is based on a clear rule specified in advance. A critical value.
  • This makes the decision straightforward + transparent
  • Helps avoid personal bias:put more weight on the evidence that supports our prejudices.

Making a decision: decision rule/Critical value

• The Critical value is a threshold that determines if the test statistic is large enough to reject the null.
  • Recall, we start assuming the null is true.
  • Then we need to test if our evidence (estimates) is different enough from the null to reject it.
  • The critical value is what determines how different is different enough.
• Null rejected if the test statistic is larger than the critical value

Making a decision: Possible outcomes

• Some times we are right:
  • Reject the null when it is false,
  • or do not reject the null when it is true.
• But, We can be wrong:
  • Reject the null even though it is true
  • or do not reject the null even though is false.

	\(H_0\) is true	\(H_0\) is false
Do not reject \(H_0\)	Correct	False negative (Type II)
Reject \(H_0\)	False positive (TYPE I)	Correct

Making a decision: Error of type I and II

• Both types of errors are wrong but

• During Testing the null is protected: we only reject it if there is enough evidence against it.

• The background assumption

  • wrongly rejecting the null (a false positive) is a bigger mistake than wrongly accepting it (a false negative).

• Decision rule (critical value) is chosen in a way that makes false positives rare.

Making a decision: Critical values

• A commonly applied critical value for a t-statistic is ±2 (or 1.96), a 95% confidence level, or a 5% level of significance (alpha).

• Other critical values can be set: 10% (1.65), 1% (2.58), etc.

• That choice of 5% means that we tolerate a 5% chance for being wrong when rejecting the null (1/20).

Making a decision: In a picture

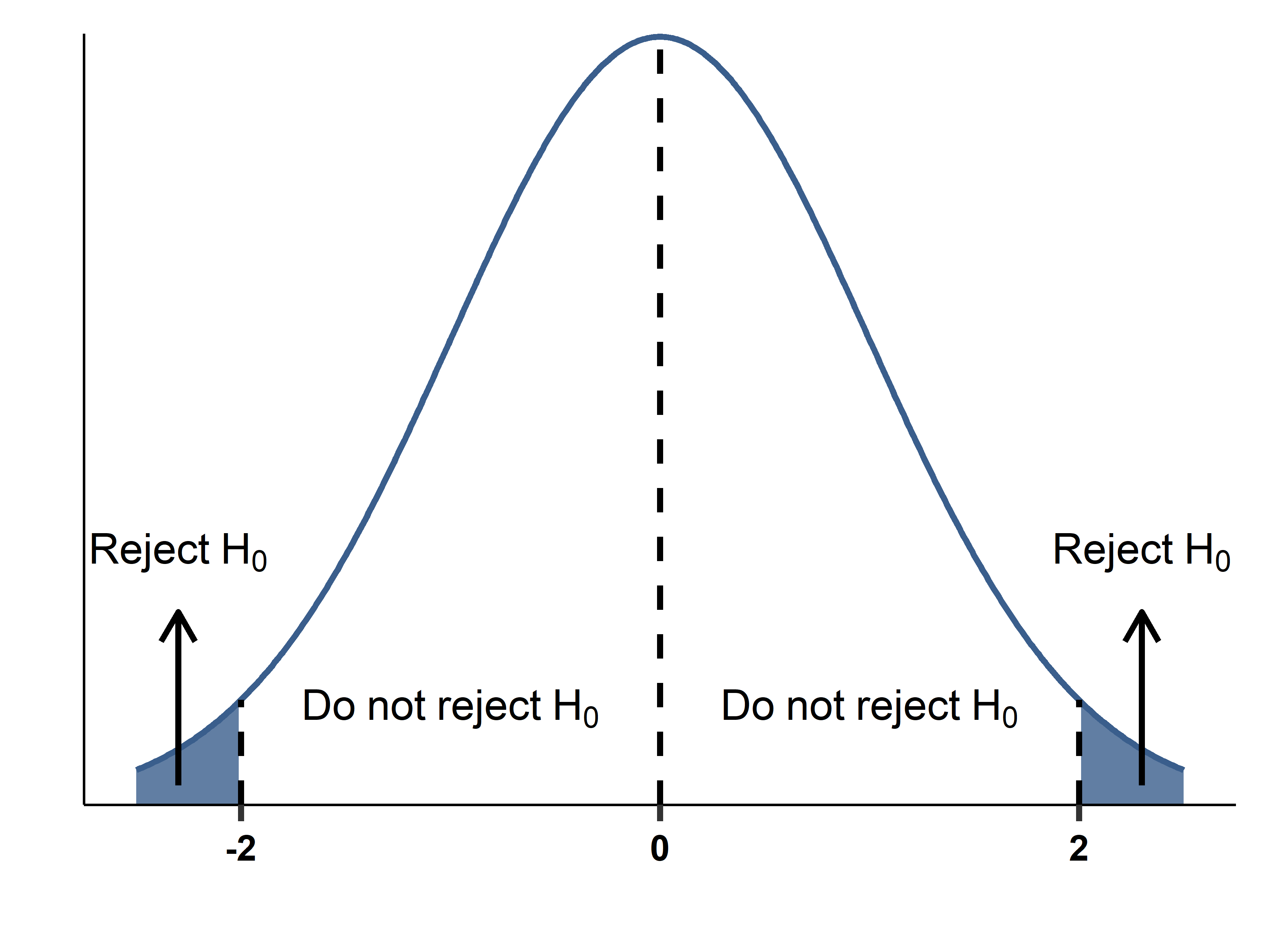
False negative (FN) and False positive (FP)

• Fixing the chance of FP affects the chance of FN at the same time.
• A FN arises when the t-statistic is within the critical values and we don’t reject the null even though the null is not true.
• This can happen if Sample is small or The difference between true value and null is small

Size and power of the test

Under the null:

• Size of the test: the probability of committing a false positive.
• Level of significance: The maximum probability of false positives we tolerate.

Under the alternative:

• Power of the test: the probability of avoiding a false negative
• Highpower is more likely if:
  • The sample size is large
  • The null is far from the true value
  • The standard error is small

Recap

• In hypothesis testing we make decisions by a rule
  • A false positive: decision to reject the null when it is true.
  • A false negative: decision not to reject the nullwhen it is false.
• The level of significance is the maximum probability of a false positive that we tolerate (\(\alpha\)=5%).
• The power of the test is the probability of avoiding a false negative.
  • In statistical testing we fix the level of significance of the test to be small (5%, 1%) and hope for high power (based on design).
• Tests with more observations have more power in general.

The p-value

The p-value

• The p-values are an alternative approach to do hypothesis testing.
  • Before we choose a critical value for a given “significance level” (5%, 1%, etc).
  • This approach suggests using the model significance.
    • The smallest significance level at which we can reject \(H_0\) in the data
    • or largest probability of a false positive that we can tolerate.
• Calculatiion Will depend on the test statistic and sampling distribution.
• Remember, you can never be certain! (P is never zero)

What p-value to pick?

• p-value is about a trade-off. Large (10-15%) or small (1%) depends on scenarios
• Guilty beyond reasonable doubt? (life or death scenario)
  • Pick a conservative value, like 1% or lower
• Proof of concept? (a new idea, a new product)
  • It’s great if it works at 5%, but even 10-15% means it’s much more likely to be true

Case Study - Comparing online and offline prices: Testing hypotheses

• Let’s fix the level of significance at 5%.
  • The value of the statistic in the dataset is -0.054. Its standard error is 0.124.
  • The t-statistic is 0.44. This is well within ±2.
• Don’t reject the null hypothesis of zero difference.
• The p-value of the test is 0.66.
• So we don’t reject the null
• We have not “proven” that online and offline prices are the same, but we have not found evidence that they are different.

Multiple test

Multiple testing: motivation

• Medical dataset: data on 400 patients
• A particular heart disease binary variable and 100 feature of life style (sport, eating, health background, socio-economic factors)
• Look for a pattern – is the heart disease equally likely for poor vs rich, take vitamins vs not, etc.
• You test one-by-one
• You find that for half a dozen factors, there is a difference
• is there any problem with this procedure?

Multiple testing

• The pre-set level of significance / p-value are defined for a single test
• but, In many cases, you will consider doing many many tests.
  • Different measures (mean, median, range, etc)
  • Different products, retailers, countries
  • Different measures of management quality
• For multiple tests, you cannot use the same approach as for a single one.
• You need to be even more conservative in rejecting the null.

Multiple testing: Example

• Consider 100 tests. The Nulls are true for all tests.
• Set \(\alpha\)=5% for each test.
• In the data, even if the null is true, you will reject 5% of the time. (false positives)
• However, if you do “use the evidence” from all tests, it would seem that the null is false in 99.4% of the cases. (by chance)
  • This is p-hacking. Choosing what works!

Multiple testing: Example

• There are various ways to deal with probabilities of false positives when testing multiple hypotheses.
  • Often complicated.
• Possible Solution: If you have a few dozens of cases, just use a strict criteria (such as 0.1-0.5% instead than 1-5%) for rejecting null hypotheses.
• A very strict such adjustment is the Bonferroni correction that suggests dividing the single hypothesis value by the number of hypotheses.
• Other methods exists, but are similar in spirit.
• Risk: by being more conservative, you are more likely to obtain false negatives.

Summary

Testing in statistics means making a decision about the value of a statistic in the general pattern represented by the data.

• Hypothesis starts with explicitly stating \(H_0\) and \(H_A\).
• A statistical test rejects \(H_0\) if there is enough evidence against it; otherwise it does not reject it.
• Testing multiple hypotheses at the same time is a tricky business; it pays to be very conservative with rejecting the null.