Main takeaways
- Regressions with time series data allow for additional opportunities, but they pose additional challenges, too
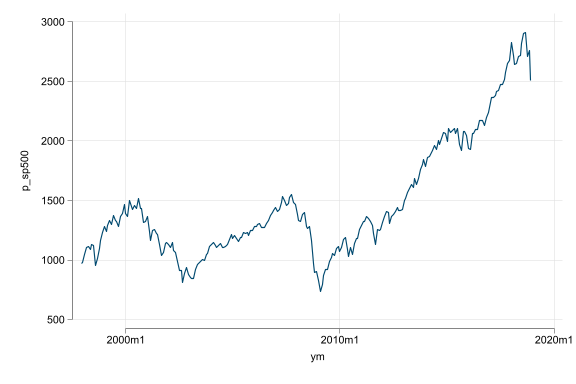
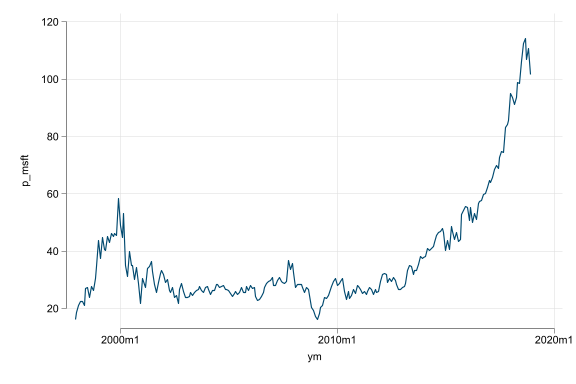
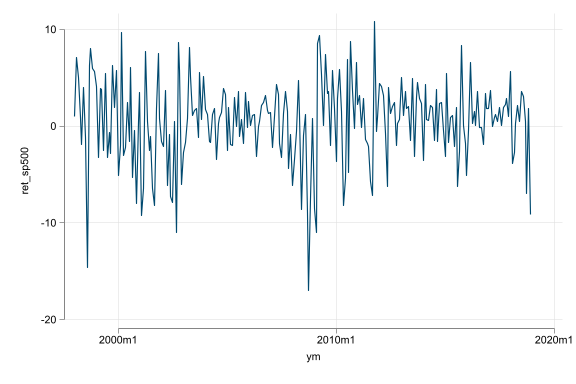
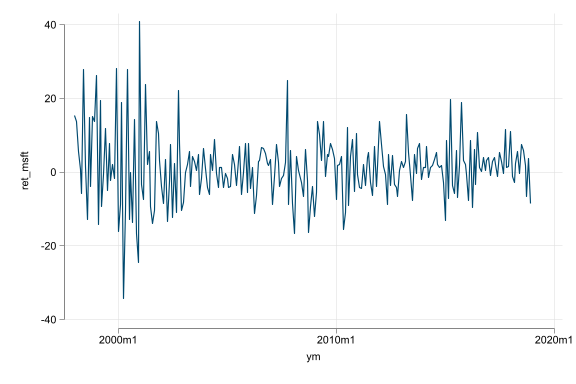
- Regressions with time series data help uncover associations from changes and associations across time
- Trend, seasonality, and random walk-like non-stationarity are additional challenges
- Do not regress variables that have trend or seasonality; without dealing with them they produce spurious results