The Mathematics of Dungeons and Dragons: A Statistical Adventure

Introduction

Dungeons and Dragons (D&D) is a popular tabletop role-playing game that has captivated players for decades. This report explores the mathematical underpinnings of D&D, focusing on the probability distributions of dice rolls and their impact on gameplay. We will examine the statistical nature of character abilities, combat outcomes, and skill checks, providing insights into the game’s mechanics through equations, data visualization, and tabular analysis.

Main Body

The Probability of Adventure

At the heart of D&D lies the rolling of dice, particularly the iconic twenty-sided die (d20). The probability of rolling any number on a d20 is uniform, but the outcomes of these rolls can be modified by character abilities and situational modifiers. The probability of success for any given action can be expressed as:

\[ P(success) = \frac{21 - (DC - modifier)}{20} \tag{1}\]

Where DC is the Difficulty Class of the task, and the modifier is the character’s relevant skill or ability modifier. This equation (Equation 1) forms the foundation of many D&D mechanics¹.

Visualizing Character Ability Scores

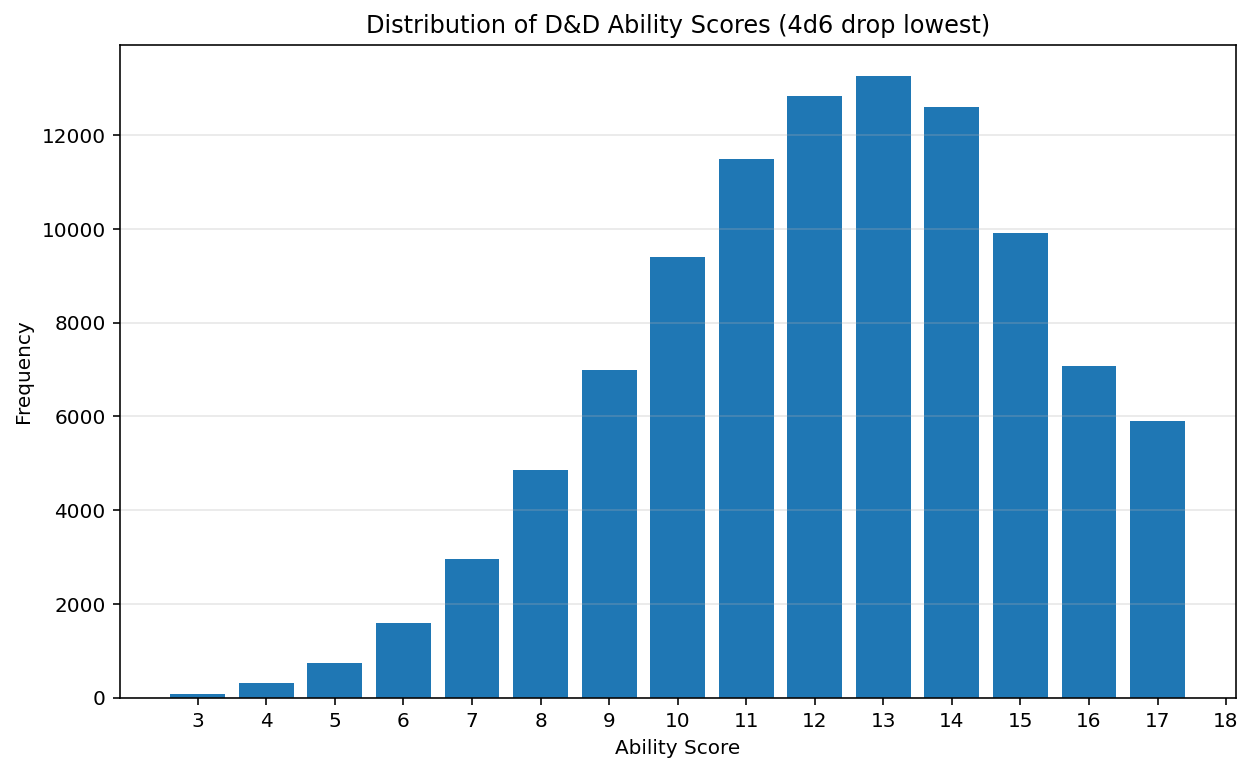
Character creation in D&D often involves rolling dice to determine ability scores. The most common method is rolling 4d6 and dropping the lowest die. Let’s visualize the distribution of these rolls:

Figure 1: Distribution of D&D Ability Scores (4d6 drop lowest)

Figure Figure 1 illustrates the distribution of ability scores using the 4d6 drop lowest method. This bell-shaped curve demonstrates why most characters have average abilities, with exceptional scores being rare.

Combat Outcomes

Combat in D&D involves a complex interplay of attack rolls, damage calculations, and defensive abilities. Table Table 1 summarizes the average damage output for different weapon types:

Table 1: Average Damage Output by Weapon Type

Weapon Type	Average Damage	Critical Hit Chance
Dagger	2.5	5%
Longsword	4.5	5%
Greataxe	6.5	5%

As shown in Table 1, weapon choice significantly impacts potential damage output, with larger weapons generally dealing more damage at the cost of other factors like weight and required strength.

The Role of Randomness

While skill and strategy play crucial roles in D&D, the element of chance introduced by dice rolls adds excitement and unpredictability to the game. According to Tormey (2019), this balance between player agency and random chance is what makes D&D both challenging and engaging. The interplay between player decisions and dice rolls creates a unique narrative experience in each game session.

Conclusion

This report has explored the mathematical foundations of Dungeons and Dragons, examining probability distributions, visualizing ability score generation, and analyzing combat mechanics. We’ve seen how equations like Equation 1 govern the core mechanics of the game, while visualizations like Figure 1 provide insights into character creation. The balance of strategy and randomness, exemplified by the combat data in Table 1, contributes to the enduring appeal of D&D as both a game and a storytelling medium.

References

Tormey, Warren. 2019. “Players and Pupils: The Pedagogical Value of Dungeons and Dragons.” Teaching English in the Two-Year College 46 (4): 343–56.

Footnotes

1. This simplified equation assumes a linear probability distribution and does not account for critical successes or failures, which are typically represented by rolling a natural 20 or 1, respectively.