Forecasting from Time Series Data

Todays forcast it will be sunny with a chance of rain

Author
Affiliation

Fernando Rios-Avila

Levy Economics Institute

Published

December 2, 2024

Forecast setup

It is difficult to make predictions, especially about the future. (Niels Bohr; possibly an old Danish proverb)

  • It is fairly easy to make forecasts for variables that have a decently stable pattern over time
    • Weekly FastMovingGoods product sales, sensor of gadgets used regularly
  • It is very hard to make forecasts of really interesting variables
    • GDP with Recession, crisis,
    • High tech gadgets with new products
    • Stock market prices
  • why???
    • Tradition!

Forecasting basics

  • Forecasting is a special case of prediction.
  • Forecasting makes use of time series data on \(y\), and possibly other variables \(x\).
  • The original data used for forecasting is a time series from 1 through \(T\), such as \(y_1, y_2, ..., y_T\)
  • The forecast is prepared for time periods after the original data ends, such as \(\hat{y}_{T+1}, \hat{y}_{T+2}, ..., \hat{y}_{T+H}\). This is the live time series data.

Forecast horizon

  • What is it?
    • The length of the live time series data (here \(H\)) = the forecast horizon.
  • Short-horizon forecasts are carried out for a few observations after the original time series;
    • 5-10 years of monthly data \(\rightarrow\) forecast a 3-12 months ahead
    • 10 years of quarterly data \(\rightarrow\) predict ahead of a few quarters
  • Long-horizon forecasts are carried out for many observations.
    • Often: data on activity, operation
    • 5 years of daily data \(\rightarrow\) forecast daily ahead for a year
    • 2 months of hourly activity data \(\rightarrow\) predict weeks ahead

Cross-validation in time series

  • Cross-validation is essential in time series
    • The ability to build a model that works well for the future, without overfitting
  • But it is tricky
    • you cannot just randomly split the data.
      • Time series is time dependent
    • But there are Options

Cross-validation: Options

  • OP1: Select a “test set” of few periods where to evaluate the model
    • Use all information before and the test set to build the model
    • And a common “end of sample” test set
    • Good for long-horizon forecasts
  • OP2: Select a “test set” of few periods where to evaluate the model
    • Use “X” periods before the test set to build the model
    • Repeat with the next Window
    • Good for short-horizon forecasts

Cross-validation

Message:

  • The strategy for prediction and cross-validation depends on the forecast horizon.
    • For short-horizon forecasts, you really need to consider the time dependence of the data.
    • For long-horizon forecasts, you try to capture long-term patterns in the data.

Long-horizon:

Seasonality, trend and predictable events

Long-horizon forecasting: Seasonality and predictable events

  • Look for aspect of data that matter for long time
  • Focus on predictable aspects of time series
    • Trend(s) + Seasonality + Other regular events
  • Two options to model trend: estimate average change or trend line
    • \(y = f(T,S,E)\) or
    • \(\%\Delta y \text{ or } \Delta y =g(T,S,E)\)
  • Seasonality: ie model with set of variables (11 months), maybe interactions
  • Other regular events - set of binary vars (War, Covid, New Policy, etc)

Long-horizon forecasting: Growth rates

First model - estimate average change:

\[\hat{\Delta}y = \hat{\alpha}\]

For prediction this means:

\[ \begin{aligned} \hat{y}_{T+1} &= y_T + \hat{\Delta}y \\ \hat{y}_{T+2} &= \hat{y}_{T+1} + \hat{\Delta}y = y_T + 2 \times \hat{\Delta}y \\ \dots \\ \hat{y}_{T+H} &= y_T xx+ H \times \hat{\Delta}y \end{aligned} \]

Long-horizon forecasting: Trends - compare options

  • Difference in models
    • Model changes:
      • Assumes that \(y\) continues from the last observation, and increase by the same amount each time. What if Last observation is unusual?
    • Model trend line
      • Assumes that \(y\) remains close to the trend line. Last unusual observation would not matter for the forecast, because it would be the trend line.
  • Neither approach is inherently better than the other

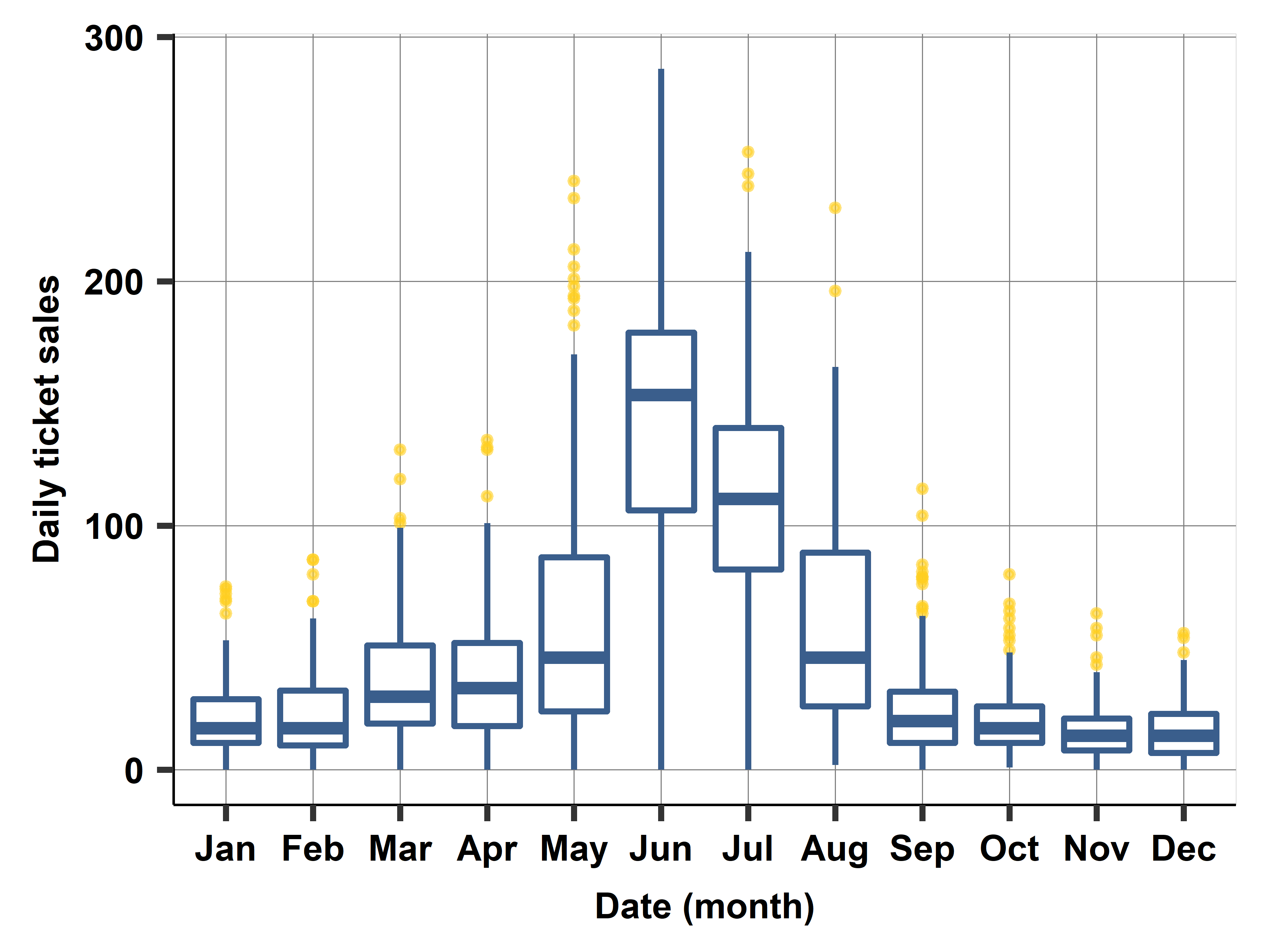
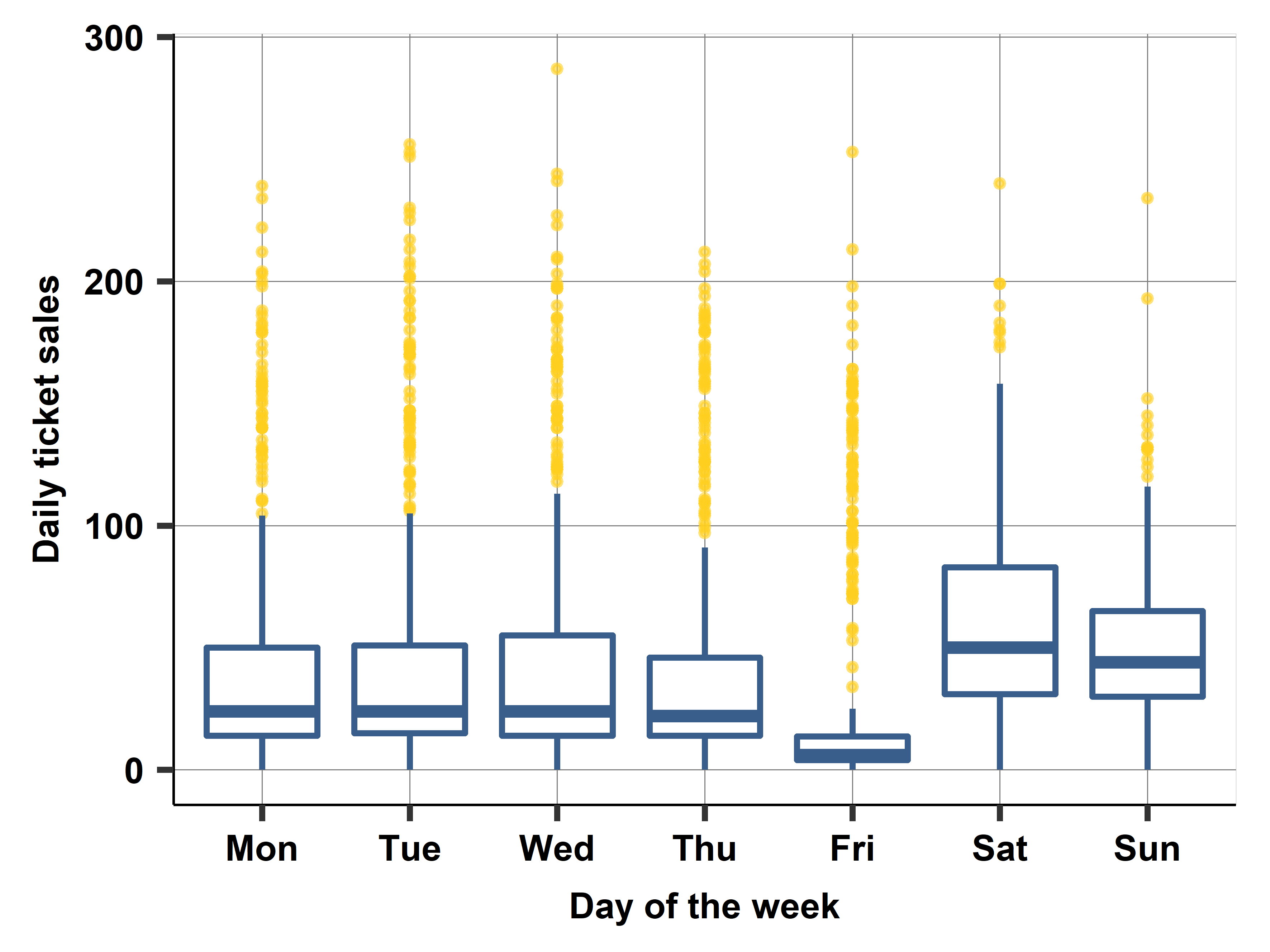
Long-horizon forecasting: Seasonality

  • Capture regular fluctuations
  • Months, days of the week, hours, combinations

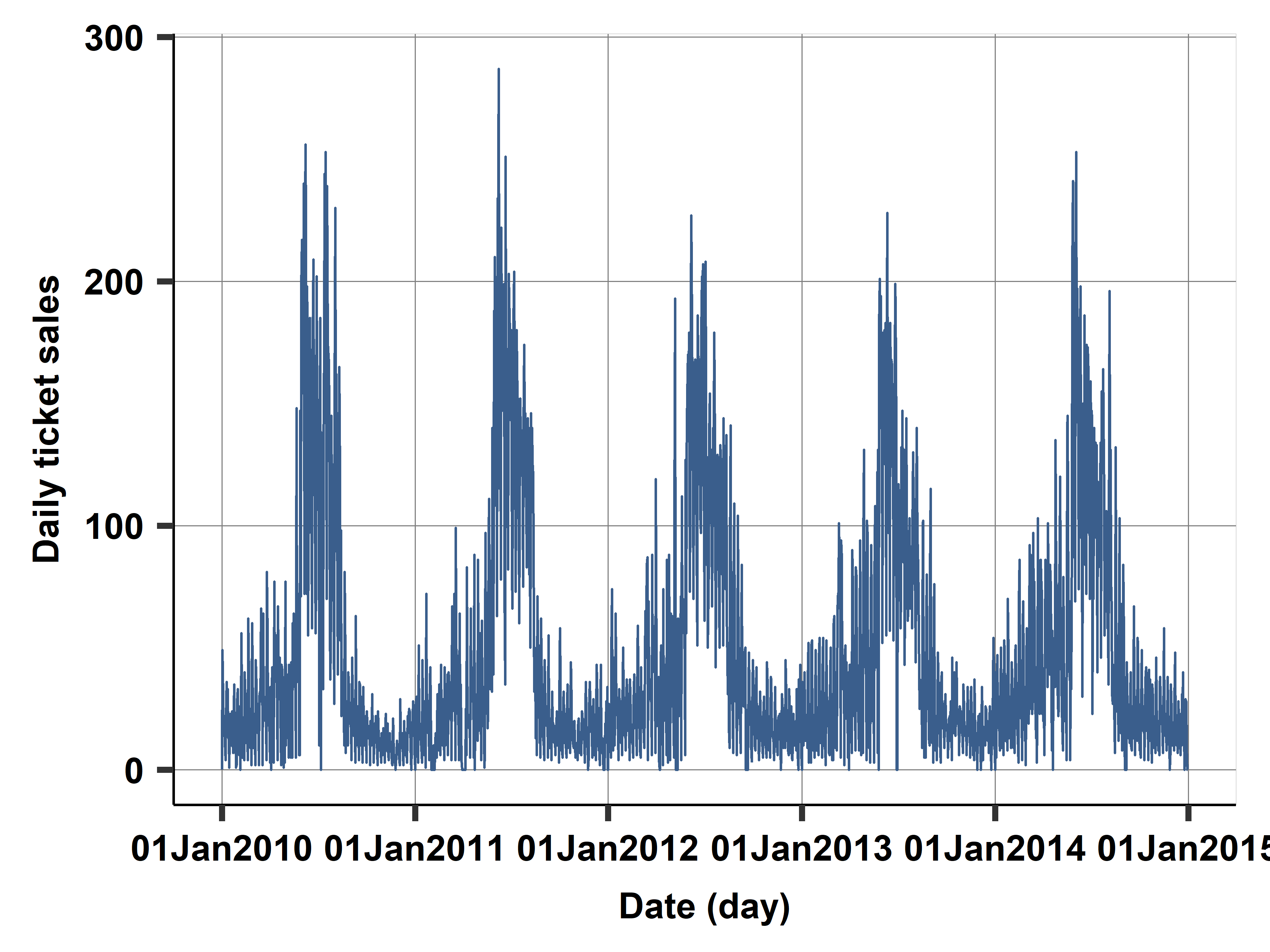
Case study: ABQ swimming

  • Swimming pool data
  • Albuquerque (ABQ), New Mexico, USA
  • Big data, transaction level entry data logged from sales systems
  • 1.5m observations

This CS:

  • Sample: Single swimming pool
  • Aggregated: number of ticket sales per day
  • After some sample design - regular tickets only

Case study: Modelling

  • Trend is simple – use simple linear trend: \(\alpha t\)
    • Maybe not really important at all
    • Perhaps consider exponential trend? (log-linear model)
  • Seasonality is important and tricky

Case study: Daily ticket sales

Daily Sales 5Yrs

Case study: Monthly and daily seasonality

Month

Day of the Week

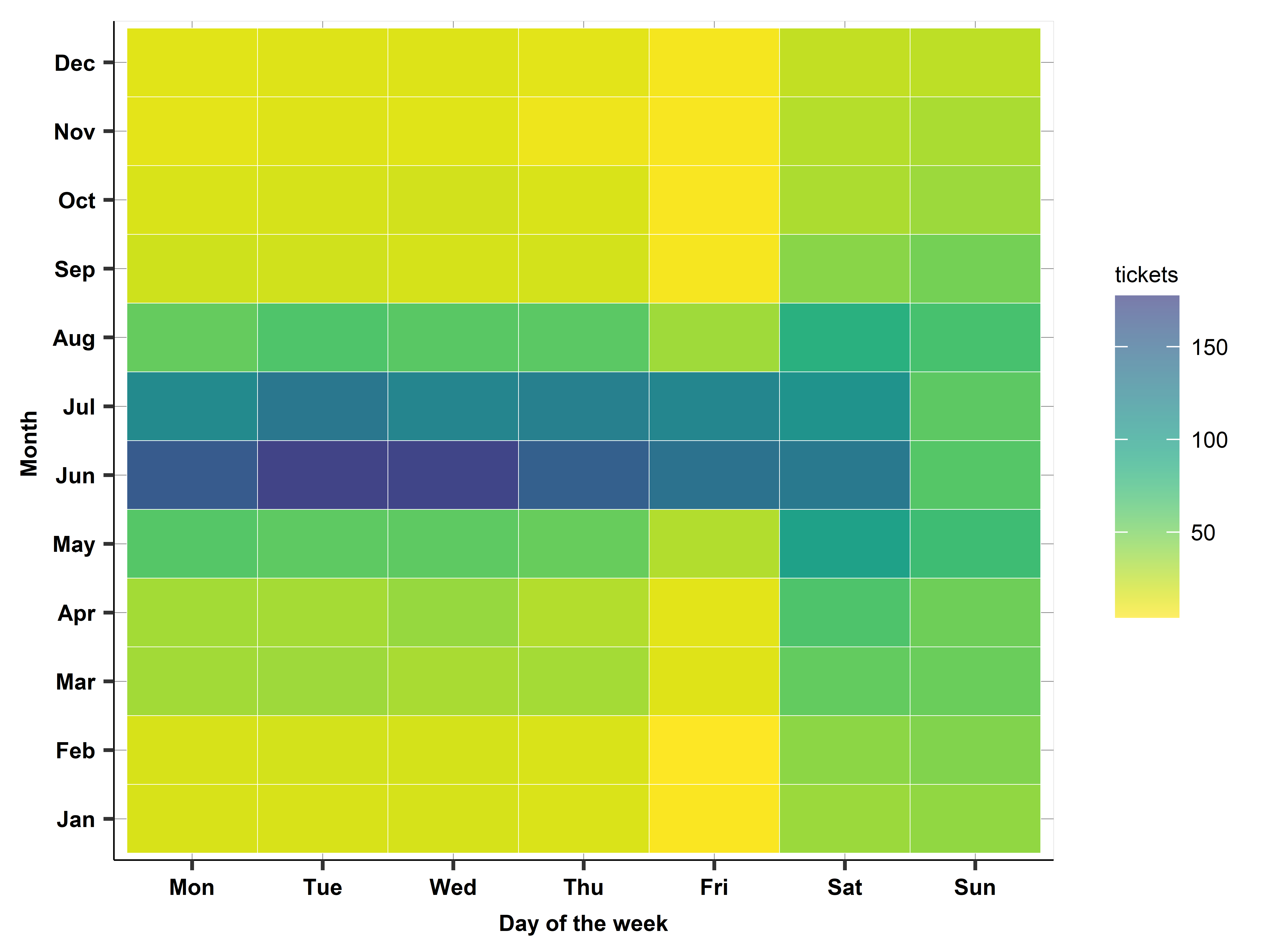
Case study: Daily ticket sales: A heatmap

  • Tool to model seasonality
  • Each cell is average sales for a given combination of day and month over years
  • Colors help see pattern

Case study: Modeling

  • Trend is simple - linear trend
  • Seasonality is tricky - need to model and simplify
    • Months
    • Days of the week
    • USA holidays (dummies)
    • Summer break (depends?)
    • Interaction of summer break and day of the week
    • Interaction of weekend and month

Case study: Model features and RMSE

trend months days holidays school*days days*months RMSE
M1 X X 32.35
M2 X X X 31.45
M3 X X X X 29.46
M4 X X X X X 27.61
M5 X X X X X X 26.90
M6 (log) X X X X X 30.99
M7 (Prophet-ML) X X X X N/A 29.47

Note: Trend is linear trend, days is day-of-the-week, holidays: national US holidays, school*days is school holiday (mid-May to mid-August and late December) interacted with days of week.
RMSE is cross-validated.
Source: swim-transactions dataset.
Daily time series, 2010–2016, N=2522 (work set 2010–2015, N=2162).

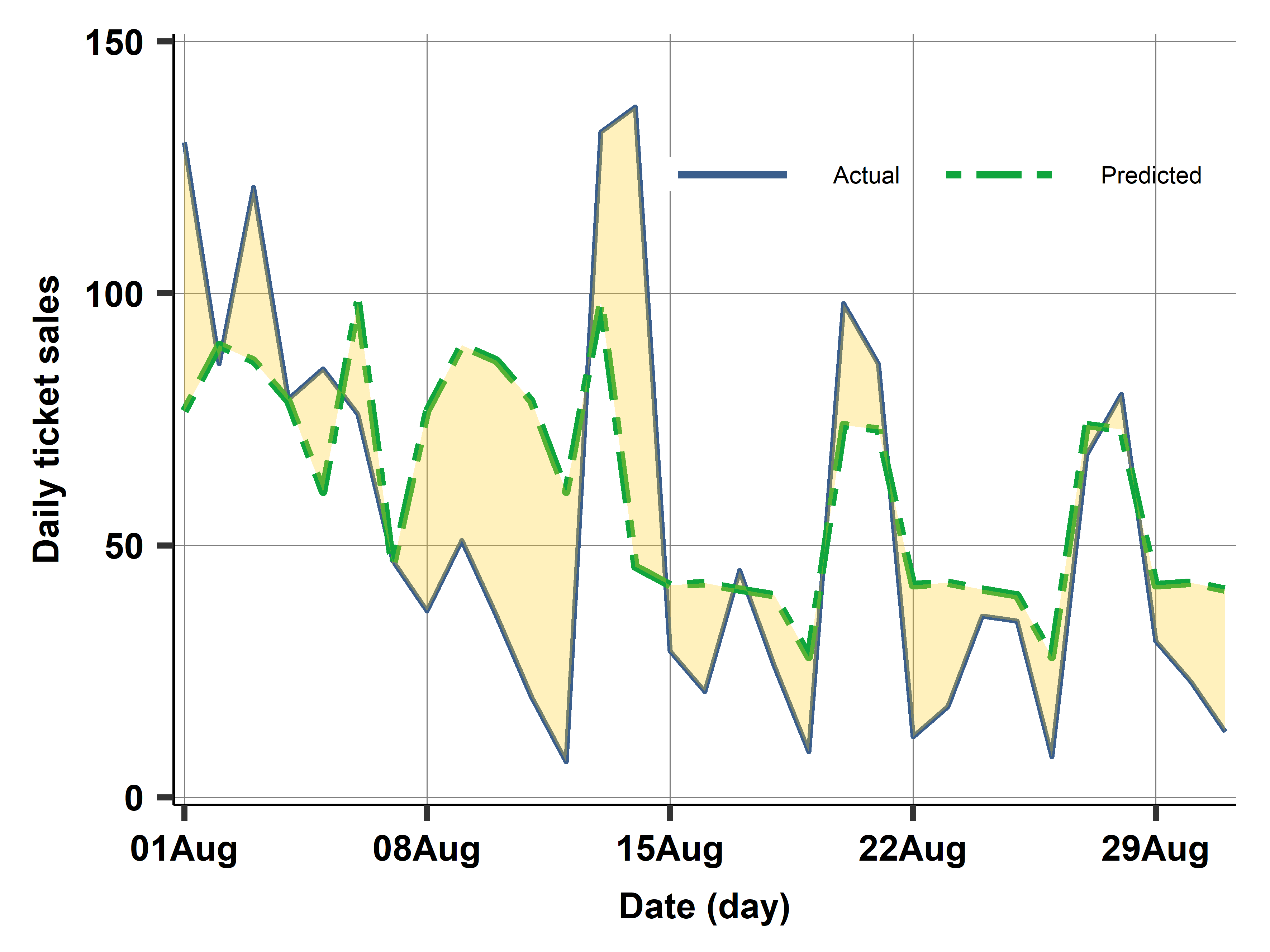
Case study: Compared actual vs predicted on holdout set (2016)

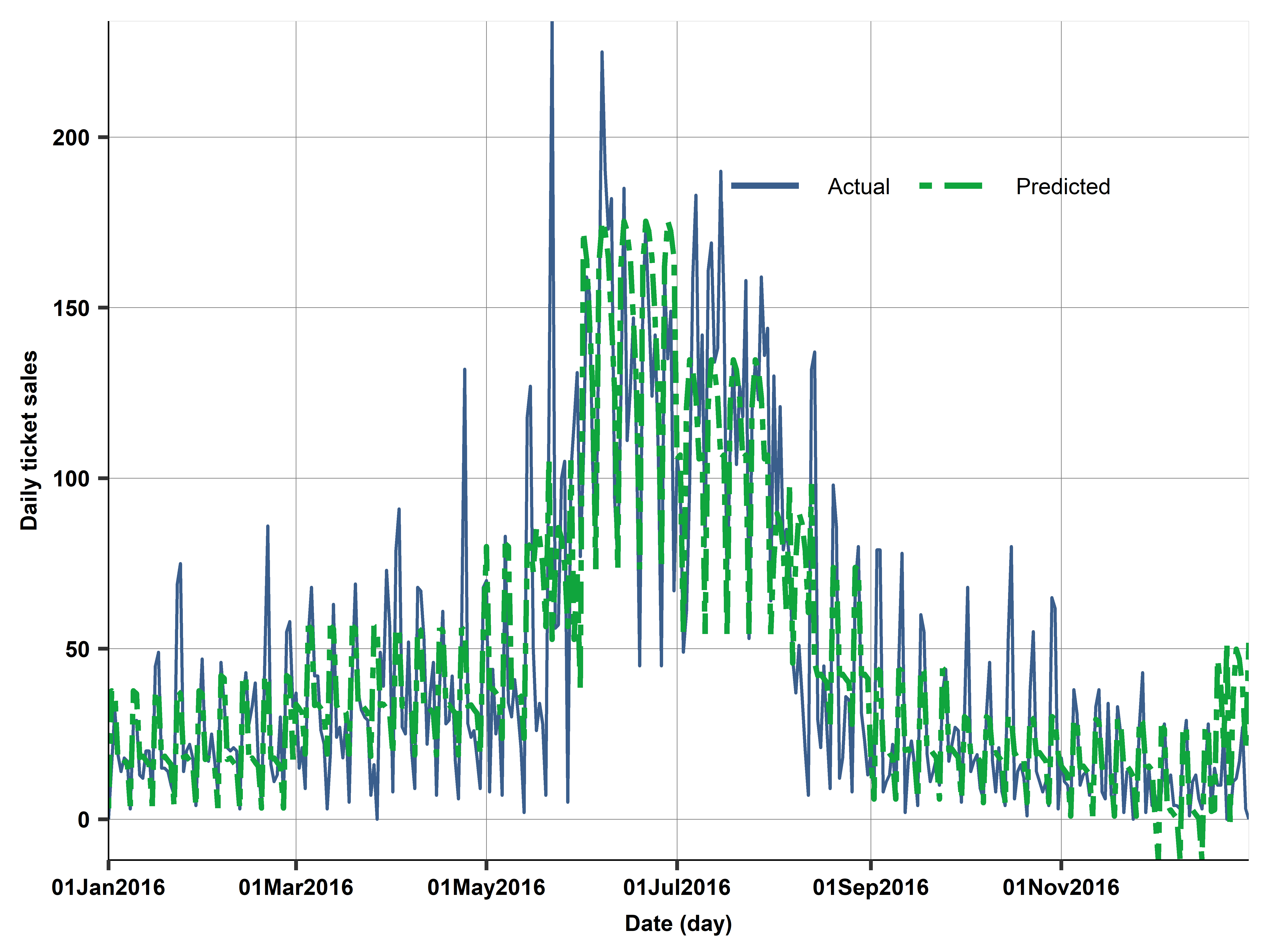
Case study: Diagnostics - holdout set (2016)

Actual vs predicted August 2016

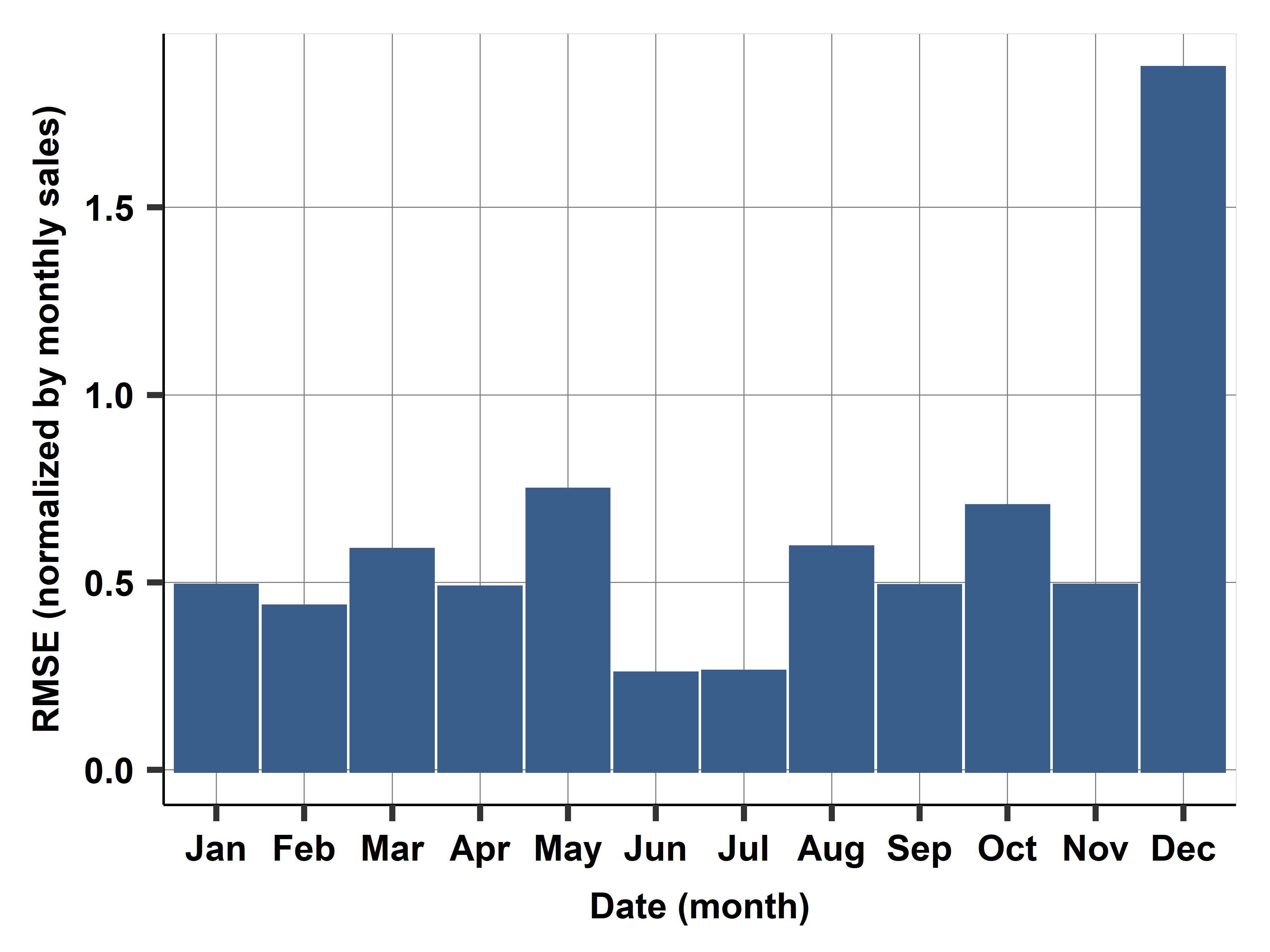
Monthly RMSE

Case study: Diagnostics vs model building

  • Here we used diagnostics to learn about what to expect, strength and weaknesses of the already selected model.
    • This means, no going back to drawing board.
  • But, we could have said, lets run some checks on the training set and maybe alter the model accordingly.
    • As we normally do with scatterplots, lowess, tabulations, etc
    • Here: something weird happening in December.
  • Act, build a new model and test, etc.

Short-run horizon, serial correlation and ARIMA

What you learn today, you can use tomorrow

Short-horizon forecasting: what is new?

  • Serial correlation is essential

    • Data Depends on itself, and Errors Also Depend on Themselves

  • Modeling how a shock fades away \(\leftarrow\) Hopefully things “return to normal”

    • Autoregressive (AR) models, capture the patterns of serial correlation – \(y\) at time \(t\) is regressed on its lags, that is its past values, \(t - 1, t - 2, etc\).

  • The simplest includes one lag only, AR(1): \[y_t^E = \beta_0 + \beta_1 y_{t-1}\]

  • Interested in estimating \(\beta_1\) or \(\rho\).

    • If \(\rho = 1\) is random walk (unpredictable),
    • if \(\rho = 0\) is white noise (also unpredictable, but stable).

Short-horizon forecasting: AR(1)

  • One-period-ahead forecast from an AR(1):
    • Its a recursive formula:

\[\begin{aligned} \hat{y}_{T+1} &= \hat{\beta}_0 + \hat{\beta}_1 y_T \\ \hat{y}_{T+2} &= \hat{\beta}_0 + \hat{\beta}_1 \hat y_{T+1} \\ &= \hat{\beta}_0 + \hat{\beta}_1 \hat{\beta}_0 + \hat{\beta}_1^2 y_T \\ \dots \\ \hat{y}_{T+k} &= \hat{\beta}_0 \sum_{s=1}^{k} \hat{\beta}_1^{s-1} + \hat{\beta}_1^{k} y_T \end{aligned} \]

ARIMA

Bringing the Big Guns

Short-horizon forecasting: ARIMA

  • ARIMA(p,d,q) models that are generalizations of the AR(1) model
    • can approximate any pattern of serial correlation.
  • ARIMA models are put together from three parts: AR(p), I(d) and MA(q).
  • but What are these?

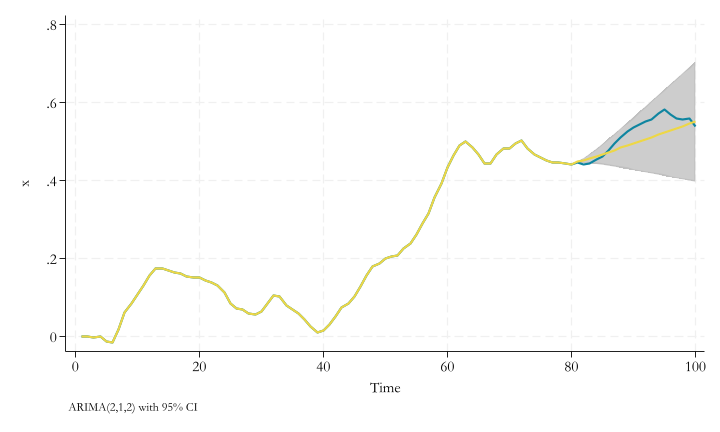
Short-horizon forecasting: ARIMA(p,d,q)

  • The ARIMA model combines three approaches to modeling time series data:
    • AR(p): autoregressive models, We have seen this
    • I(d): models of differences, This is new
      • Relates to models that you first take the difference before modeling.
      • For example \(\Delta y_t = y_t - y_{t-1} = \alpha\) is a I(1) model
    • MA(q) models: moving average models: Concentrates on the error term, and how much it “depends” on past errors.
      • For example \(y_t = e_t + \theta e_{t-1}\) is a MA(1) model
      • \(\theta\) has to be estimated via maximum likelihood, not OLS.

ARIMA: Mix and Match

  • ARIMA(2,1,0): \(\Delta y_t = \beta_0 + \beta_1 \Delta y_{t-1} + \beta_2 \Delta y_{t-2} + e_t\)
  • ARIMA(0,1,1): \(\Delta y_t = \beta_0 + \theta e_{t-1} + e_t\)
  • ARIMA(0,2,2): \(\Delta^2 y_t = \beta_0 + \theta_1 e_{t-1} + \theta_2 e_{t-2} + e_t\)
  • ARIMA(p,d,q): \(\Delta^q y_t = \beta_0 + \sum_{i=1}^{p} \beta_i \Delta^q y_{t-i} + \sum_{j=1}^{q} \theta_j e_{t-j}+e_t\)

In practice, You rarely see \(d>2\), although \(p\) and \(q\) can be larger (depending on frequency of data)

How to choose (p,d,q)?

  • Empirical approach
    • Whichever works best in a cross-validated exercise!
    • Try out a few and pick the one that works best
    • “auto-arima” - an algo that tries out many options
    • keep it simple, \(d = 0, 1\) and \(p = 0, 1, 2\) and \(q = 0, 1, 2\) rarely more

How to choose (p,d,q)?

  • Box-Jenkins Methodology

  • Step 1: Determine \(d\). Typically you test if the data is stationary (ADF test or PP test). You difference the data until it is stationary.

  • Step 2: To determine \(p\) and \(q\) you look at the ACF and PACF of the differenced (if applicable) data.

    • ACF or Autocorrelation function
      • \(corr(y_t, y_{t-1})\), \(corr(y_t, y_{t-2})\), etc.
      • Helps Identify MA component (based on spikes)
    • PACF or Partial autocorrelation function
      • \(y_t = \beta_0 + \beta_1 y_{t-1}+ e_t\)
      • \(y_t = \beta_0 + \beta_1 y_{t-1}+\beta_2{t-2} y_{t-2} e_t\),etc
      • Helps Identify the AR component

Case study: Case- Shiller home price index

  • Case-Shiller home price index, Los Angeles
  • Monthly index of home prices
  • Data available: fred.stlouisfed.org
  • Use 18 years of monthly data

Case study: Case Shiller home price data

  • 18 years of data 2000-2017
  • work: 2000-2016, holdout is 2017
  • cross-validate with rolling window, 4-fold
    • train is 2000-2012, test is 2013
    • …
    • train is 2003-2015, test is 2016
  • Predict 12 months ahead
  • RMSE - symmetric and quadratic loss
  • Assume getting index right matters exactly the same

Case study: target variable

  • What should be the target variable?
    • The price index
    • The log of the price index
    • First difference <- Shortcut to assume I(1) process
  • We’ll try out, and pick via cross-validation
  • The model should include seasonal dummies (could be more complicated)
  • The model may include a linear trend or capture it with \(\Delta y\) as target
  • The model can have any form of ARIMA

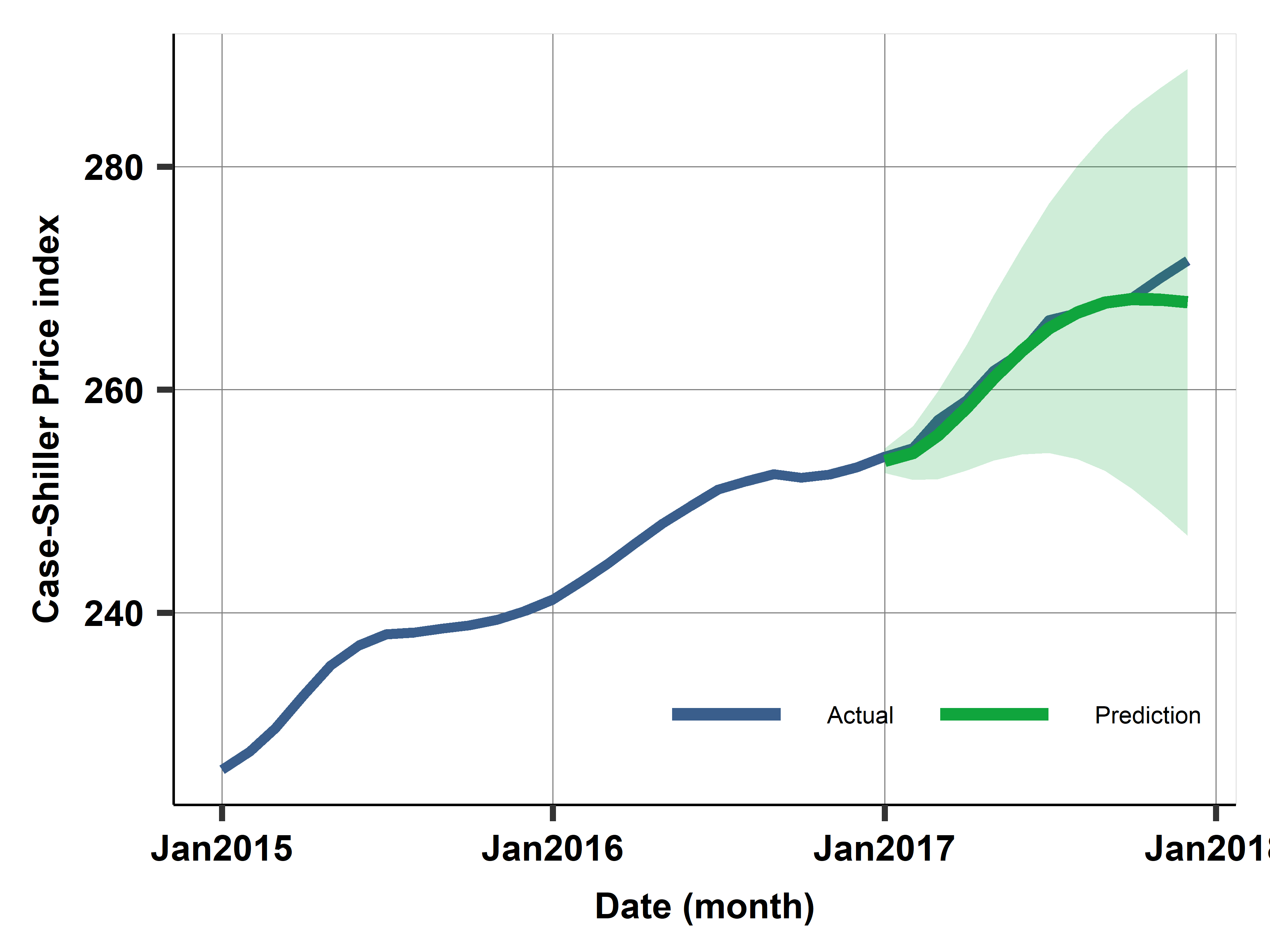
Case study: Case- Shiller home price index - prediction from ARIMA models

id target ARIMA trend season AR I MA RMSE
M1 p NO X X 31.9
M2 p YES 1 1 2 9.5
M3 p YES X 1 1 1 0 4.1
M4 p YES X X 2 0 0 2.3
M5 dp NO X X 18.8
M6 lnp YES X 0 2 0 0 7.2

Case study: Prediction with best model M4: Uncertainty

Figure 1

Stata Corner

In Stata, the easiest way to estimate ARIMA models is using arima command:

  • ARIMA(2,2,2) model: arima y, arima(2,2,2)

Predictions are a bit tricky. You can use predict command with the dynamic option to predict out-of-sample values. But also need to indicate “which” periods to start using the model predictions

  • predict yhat, dynamic(ym(2017,1)) [y]

yhat is the new variable, ym(2017,1) indicates the first period of 2017, and [y] indicates that we want to predict the “real” dependent variable. Not the changes or transformations.

No built-in option for CI predictions.

Vector Autoregression

When you need more than one variable

VAR

  • Better forecasts with the help of other variables, at least for short forecast horizons.
  • Need forecasts of the \(x\) variable as well – we need a model.
  • Vector autoregression (VAR), is a method that incorporates other variables in time series regressions and can use those other variables for forecasting \(y\).
  • Technically, you are not “ONLY” forecasting \(y\) anymore, but a set of time series regressions.
  • A set of time series regressions.

\[{y_t, x_t, z_t} =W_t= \beta_0 + W_{t-1}\beta_1 + W_{t-2}\beta_2 + \dots + W_{t-p}\beta_p + e_t \]

VAR: simplest model

The simplest VAR model has \(y\) and one \(x\) variable, and it includes one lag of each = VAR(1) model.

It assumes that all data have the same frequency. \[\begin{align*} y_t^E &= \beta_{10} + \beta_{11} y_{t-1} + \beta_{12} x_{t-1} \\ x_t^E &= \beta_{20} + \beta_{21} y_{t-1} + \beta_{22} x_{t-1} \end{align*} \]

VAR forecast

  • One-period-ahead forecast for \(y\), only need estimates from the first one: \[\hat{y}_{T+1} = \hat{\beta}_{10} + \hat{\beta}_{11} y_T + \hat{\beta}_{12} x_T \]

  • For forecasting \(y\) further ahead, we do need all coefficient estimates, and forecast values of \(x\) as well.

  • A two-period-ahead forecast of \(y\) from a VAR(1) is

\[ \hat{y}_{T+2} = \hat{\beta}_{10} + \hat{\beta}_{11} \hat{y}_{T+1} + \hat{\beta}_{12} \hat{x}_{T+1} \]

and \(\hat{x}_{T+1}\) and \(\hat{y}_{T+1}\) are from the first forecast.

Forecasts for \(T + 3, T + 4, etc.,\) are analogous.

VAR characteristics

There are four important characteristics of a VAR:

  • A VAR has a regression for each of the variables.
  • The right-hand side of each equation has all variables.
  • Right-hand-side variables are in lags only.
  • All right-hand-side variables in all regressions have the same number of lags

Note: More often than not, you need the “system” to be stable/stationary. This is a bit more complex than just checking the target variable. (You need to see the Matrix of coefficients)

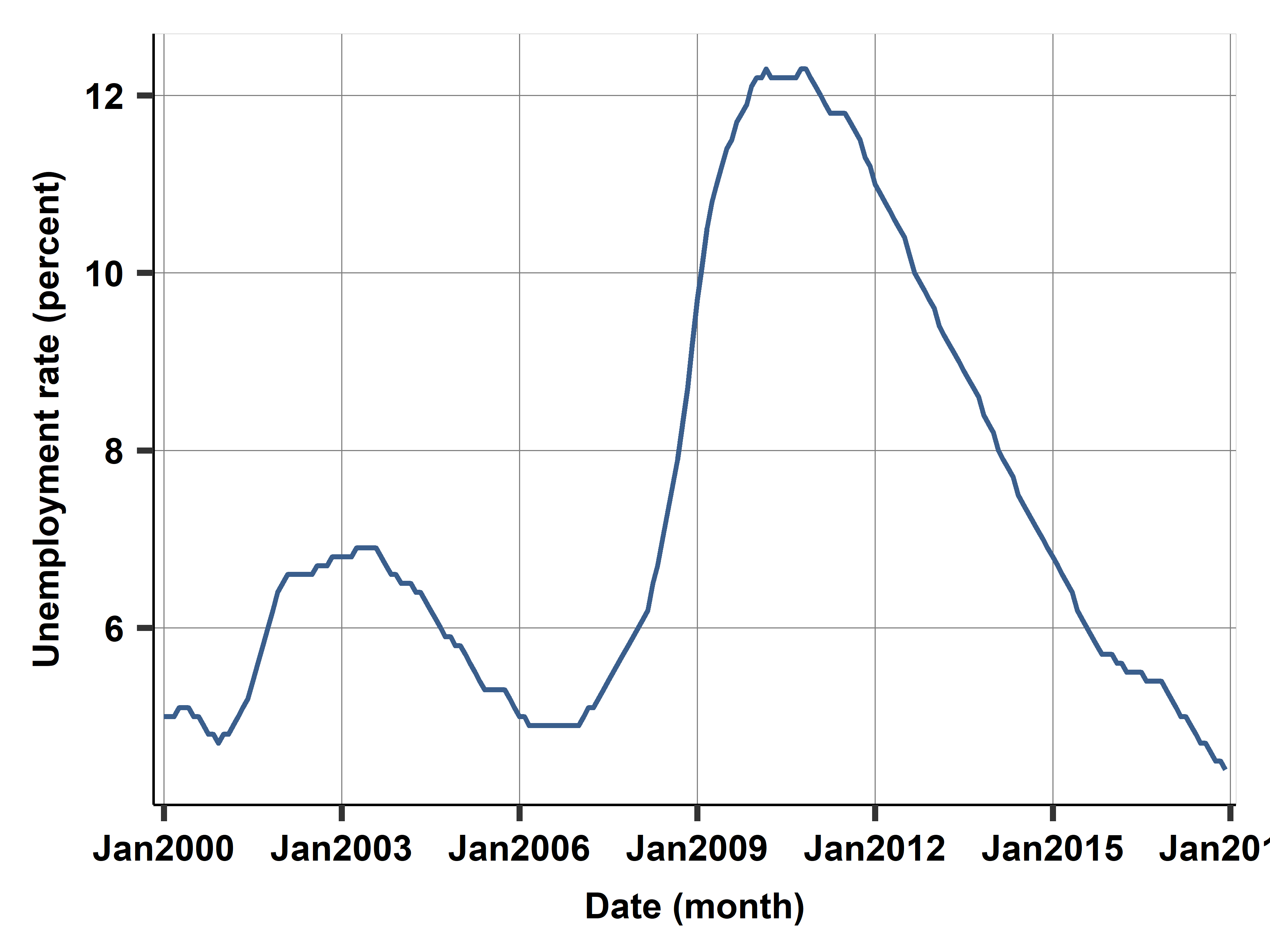
Case study: Unemployment Rate

U. Rate

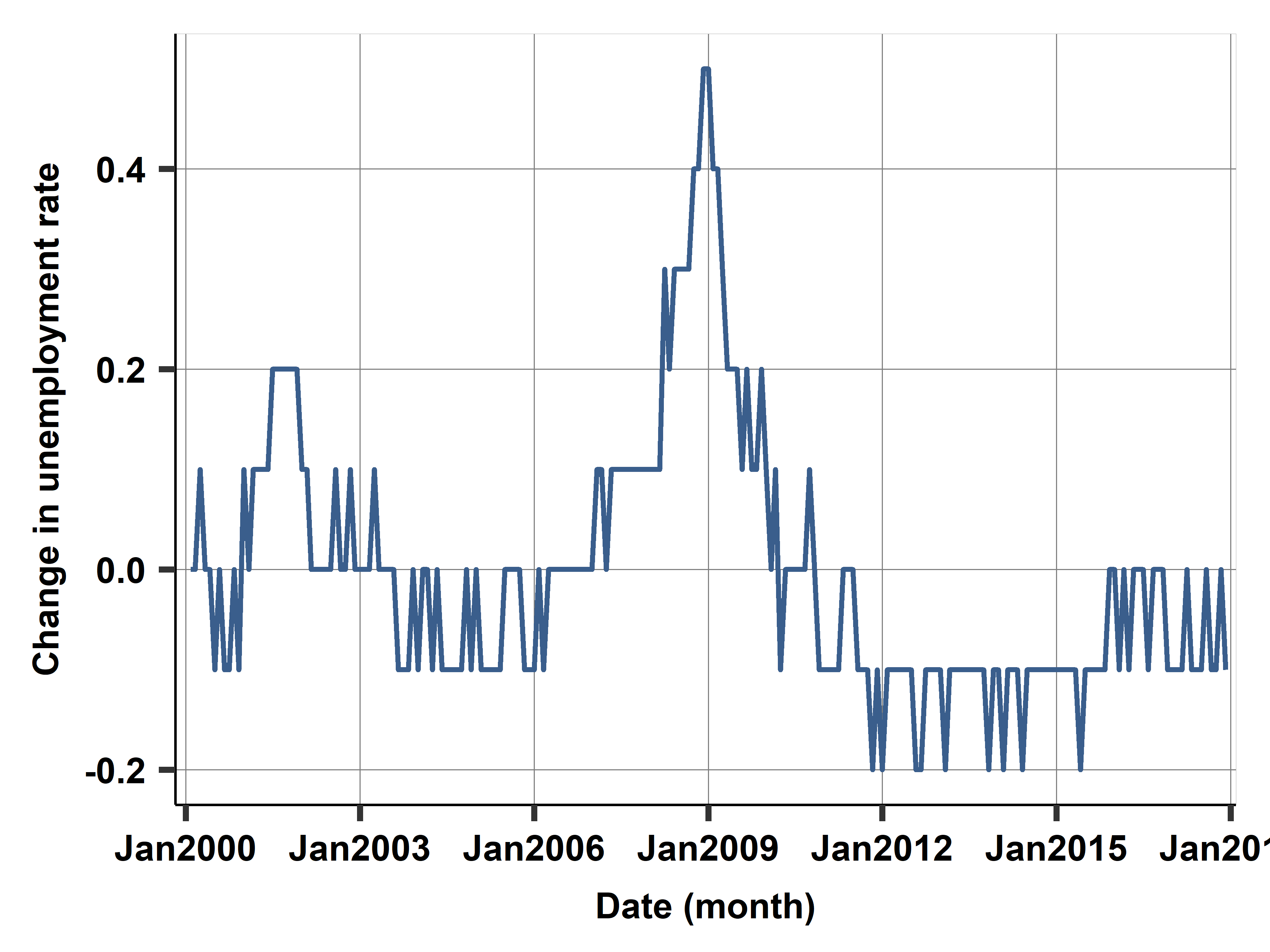
Change in U. Rate

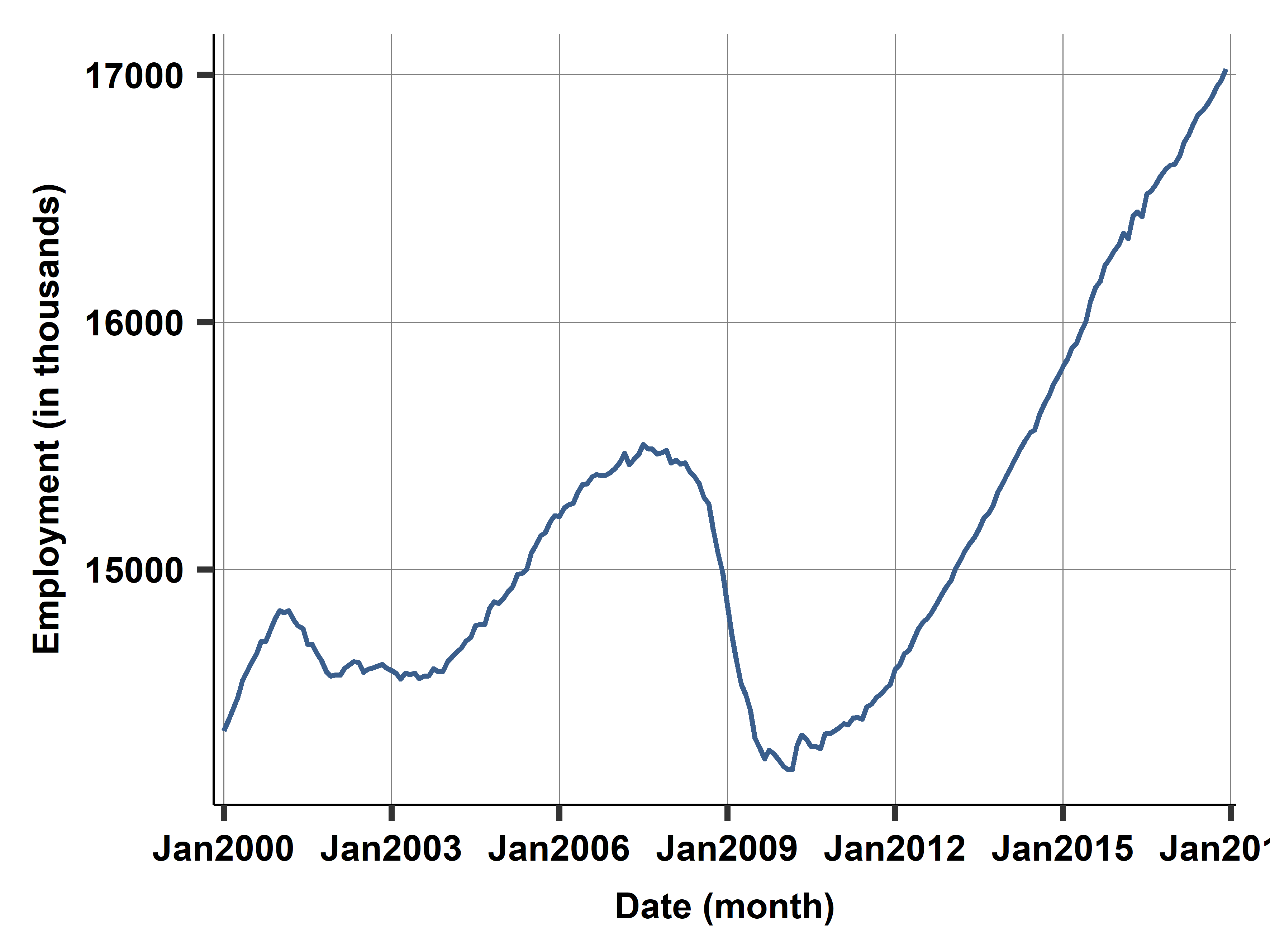
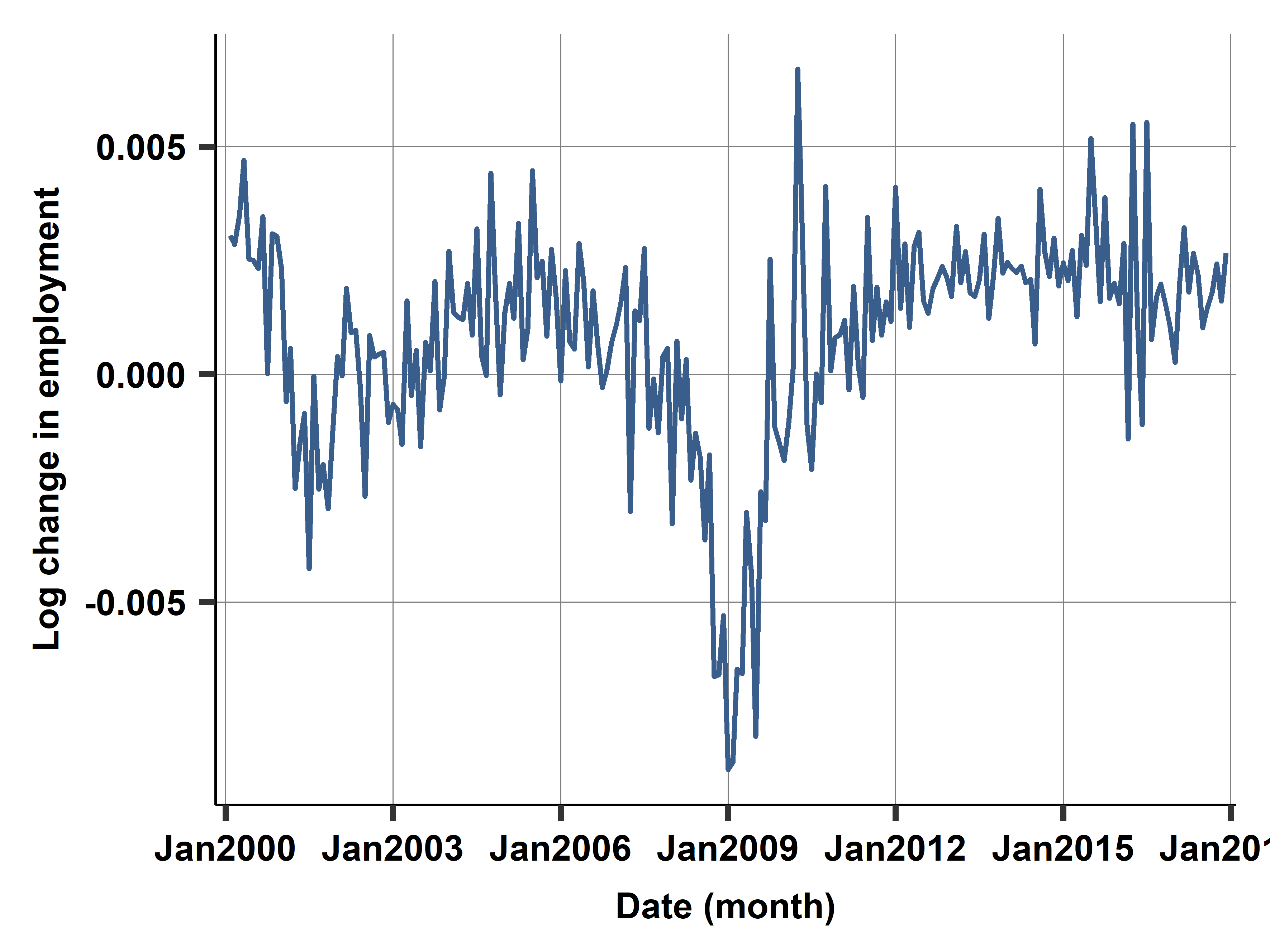
Case study: Employed Population

ln(emp)

Change in ln(emp)

Case study: Case- Shiller home price index - Model selection 2

Run the VAR model and compare to previous results.

id target ARIMA trend season AR I MA RMSE
M1 p NO X X 31.9
M2 p YES 1 1 2 9.5
M3 p YES X 1 1 1 0 4.1
M4 p YES X X 2 0 0 2.3
M5 dp NO X X 18.8
M6 lnp YES X 0 2 0 0 7.2
M7a dp VAR 7.8
M7b dp VAR X 4.5
  • In this case study, VAR did not improve on ARIMA.

VAR in Stata

Stata has a feature for the estimation of VAR models called…Var

var depvarlist [if] [in] [,lags(#) exog(varlist) Other]

  • depvarlist are all the variables one needs to analyze.

  • lags(#) indicates how many (and which) lags to use.

For prediction look into fcast, predict or forecast

External validity in time series

  • External validity is about the stability of patterns in the data

    • Such as trends, seasonality (Do they repeat? or do we need to update?)

  • Stationarity is what we look for:

    • Distribution of the target, predictors is stable over time
    • Correlation patterns also stable over time
    • We can then make predictions of the future!

  • External validity is massive risk with time series by design: predict for future

  • What if we update the model with NEW data. How well would it do?

Case study: Case- Shiller home price index - model fit on test sets

Four test set (in work set) with rolling window CV. RMSE in each test set for each model.

Fold1 Fold2 Fold3 Fold4 Average
M1 14.90 17.58 34.44 48.58 31.9
M2 14.83 8.39 6.23 5.52 9.5
M3 6.68 1.39 3.29 3.22 4.1
M4 2.22 1.96 2.88 1.20 2.2
M5 33.94 9.79 10.44 7.39 18.8
M6 2.49 4.95 9.22 9.54 7.2
M7a 13.30 5.85 3.52 4.28 7.8
M7b 5.24 2.51 5.18 4.75 4.5

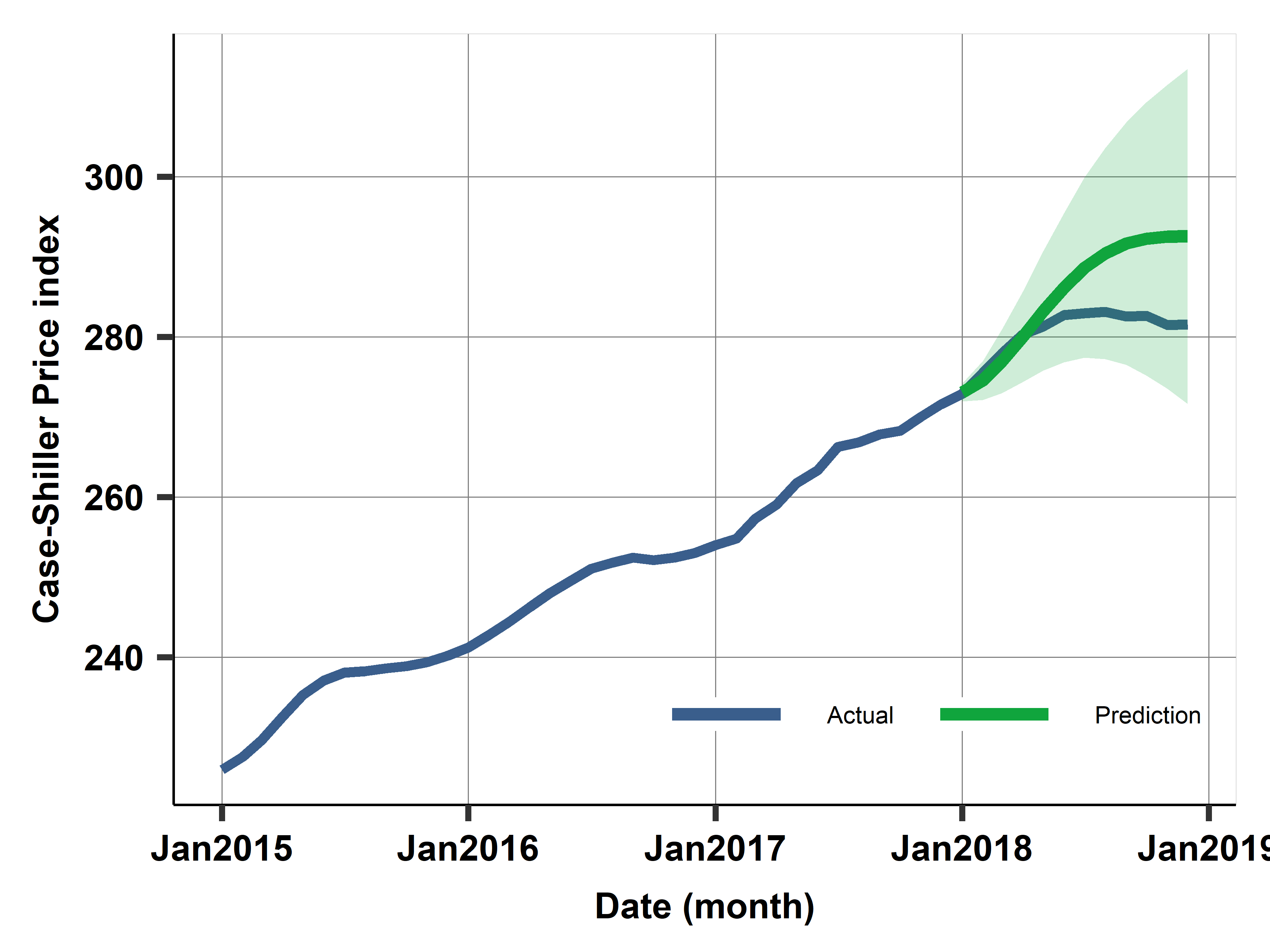
Case study: Prediction with best model M4 for 2018

Summary

  • Time series prediction is both simple and very hard
    • Simple as some basic models work okay
    • Model trend as first difference or linear trend
    • Model seasonality, regular events
    • Some basic method of capturing serial correlation
  • Time series prediction model building is also very hard
    • Getting seasonality, holidays, changing patterns right
    • Getting target variable and ARIMA(p,d,q) selection needs competing models
  • Most importantly: external validity is a huge problem
    • Stability may easily break down, and there is nothing we can do.

Extra: ARIMA with Forcast

News! I just got word from Stata Technical services regarding Arima and the Forcasting and CI.

The official word is as follows:

It is possible to obtain Confidence Intervals with arima using the forecast command. This uses simulations to obtain the CI.

Lets do an example

Extra Example

Step 1: Setup, I will simulate data for an ARIMA(2,1,2) model

Code 
clear
set seed 2
set obs 100
gen t = _n
tsset t
gen ut = rnormal()*0.01
gen dxt = 0
replace dxt =  .5 *l.dxt + .2 *l2.dxt + ut + 0.5*l.ut - 0.25*l2.ut if t>2
gen x=sum(dxt)

Step 2: Estimate the ARIMA(2,1,2) model using t=1 to 80

Code 
qui: arima x if t<=80, arima(2,1,2)  
est sto arima_est

Step 3: Forecast the next 20 periods, with 95% CI

Code 
capture forecast clear        // "clears" the last forecast
forecast create arima_predict // Sets the Forecast setup
forecast estimates arima_est, names(Dx) // Names the outcome Dx
forecast identity x = L.x + Dx // reconstructs x (the forecast)
forecast solve, prefix(f_) begin(81) ///
simulate(betas, statistic(stddev, prefix(sd_)) reps(200)) /// Forcast and does the simulation

Extra: ARIMA with Forcast

Step 4: Plot the forecast

Code 
qui replace sd_x = 0 if sd_x ==.
generate low = f_x - invnormal(0.975)*sd_x
generate up  = f_x + invnormal(0.975)*sd_x

color_style bay
two (rarea low up t, color(gs12)) (line x t , lwidth(.5) ) ///
     (line f_x t, lwidth(.5)  ),  ///
     ytitle("x") xtitle("Time") legend(off) ///
     note("ARIMA(2,1,2) with 95% CI") // Adds a note